8-ci sinif
Mövzu: Pifaqor teoremi
Standart: 3.1.3. Pifaqor teoremini tətbiq edir, iti bucağın triqonometrik funksiyalarının təriflərini bilir və bəzi bucaqların triqonometrik funksiyalarının qiymətini tapır.
Təlim məqsədi: Pifaqor teoremini mənimsəyib, məsələyə tətbiq edir.
İnteqrasiya: Fizika, informatika.
İş forması: Qruplarla iş.
İş üsulları: “Beyin həmləsi”, müzakirə.
Resurslar: Dərslik, iş vərəqləri, xətkeş, İKT
Motivasiya:
Motivasiya üçün Pifoqorun və düzbucaqlı üçbucağın əks olunduğu şəkil şagirdlərə nümayiş olunur və belə bir sual verilir: “Bu şəkil nəyi ifadə edir?”

Şagirdlər şəklə baxıb öz cavablarını-fərziyyələrini söyləyirlər. Bu fərziyyələrə istinad olunaraq tədqiqat sualı müəyyənləşdirilir:
Tədqiqat sualı:
1. Düzbucaqlı üçbucaqda katetlər məlum olduqda hipetonuz necə tapılır?
2. Hipetonuz və katetlərdən biri verildikdə digər katet necə tapılır?
Tədqiqatın aparılması:
Tədqiqatın aparılmasından öncə şagirdlərə belə bir tapşırıq verilir:
Boş xanalara uyğun ədədləri qeyd edin.
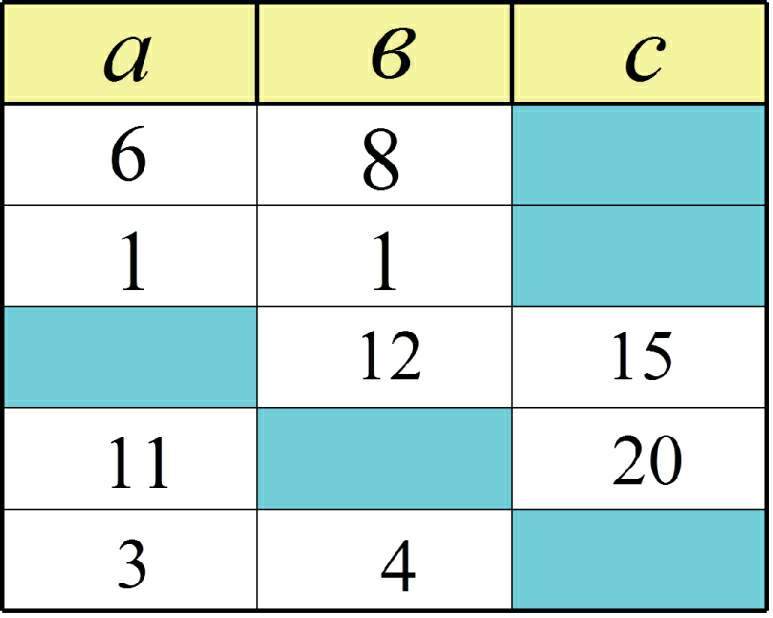
Düzgün cavablar.
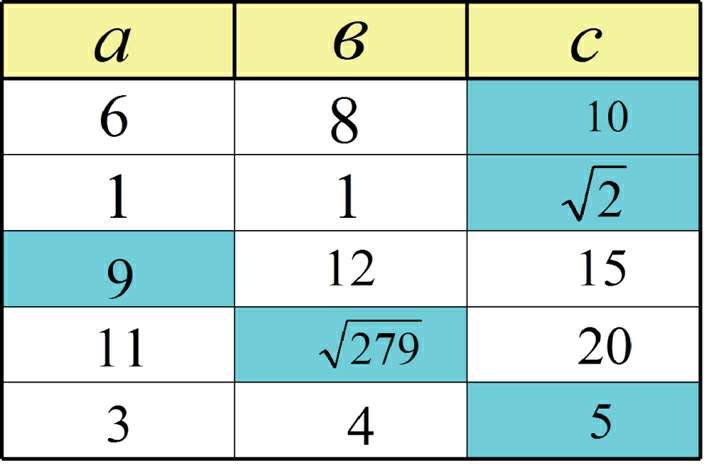
Tapşırıq yerinə yetiriləndən sonra müəllim Pifaqor haqqında məlumat verir.
Müəllimin şərhi:
Pifaqor eramızdan əvvəl 570-ci ildə Sidonda (və ya Samosda) anadan olub. Onun 490-cı ildə öldüyü güman edilir. Metafizika, riyaziyyat, musiqi, etika, siyasətə dair araşdırmalar müəllifidir.
Pifaqorun həyatı əfsanələşdirilib. Onu hətta möcüzə sahibi, peyğəmbər sayanlar da olub. Herodot Pifaqoru böyük Ellin müdriki adlandırırdı. Pifaqor öz dövrünün bütün tanınmış müdrikləri ilə görüşüb. Yunanlar, farslar, xaldeylilər, misirlilərlə təmasda olub, bəşəriyyətin topladığı bütün elmləri öyrənib. İlk təhslini Samosda alıb. Sonra bura ona darlıq edib və Miletə gedib. Burada böyük filosof Falesin tələbəsi olub. Fales daha da irəliləmək üçün ona məsləhət görüb ki, elm dalınca Misirə getsin. Pifaqor onun tövsiyəsinə əməl edib. Misirdə o vaxt matah bilikləri məxfi saxlayar, xüsusən əcnəbilərə öyrətməzdilər. Bu səbəbdən Pifaqorun başqa əcnəbilərə yasaq edilən elmləri öyrənməsinə şərait yaradılıb. Yamvlixə görə, Pifaqor ölkəni 18 yaşında tərk edib, iyirmi iki il Misirdə olub. Oradan Babilistana gedib. Öz istəyi ilə yox. 525-ci ildə xəracın vaxtında ödənmədiyini bəhanə edərək Misiri işğal edən İran şahı Kambiz Pifaqoru da əsirlərlə bərabər Babilistana aparıb. Pifaqor 12 il də Babilistanda qalıb, maqlarla ünsiyyətə girib, onlardan elm öyrənib. Nəhayət, 56 yaşında müdrik bir şəxs kimi vətənə qayıdıb.
Qədim Misir yerölçənləri düzbucaq qurmaqdan ötrü, ipi 12 bərabər hissəyə bölüb uclarını düyünləyirmişlər. Sonra ipi yerdə elə dartırlarmış ki, tərəflərdə 3, 4 və 5 düyün olan üçbucaq alınsın. 5 bölgülü tərəf qarşısındakı bucaq düz bucaq olur.
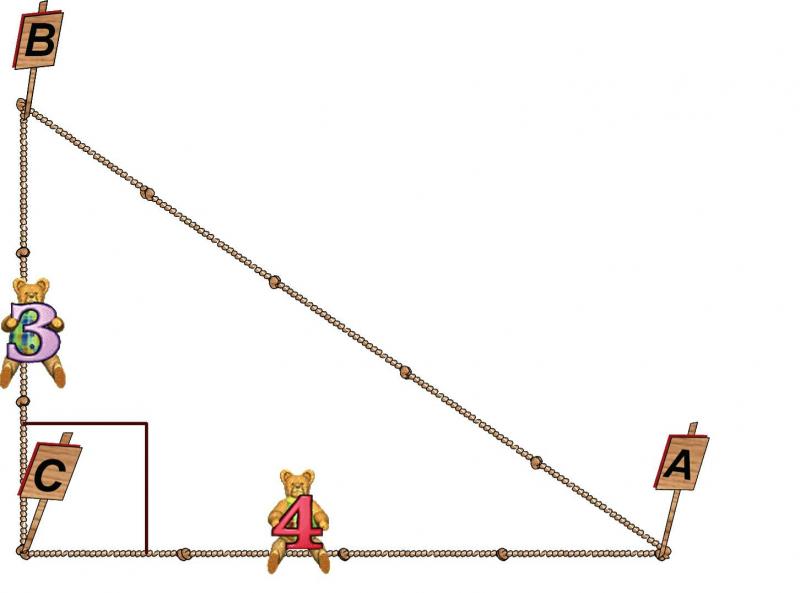
Bu üsuldan piramidaların tikilməsində də istifadə edilib.
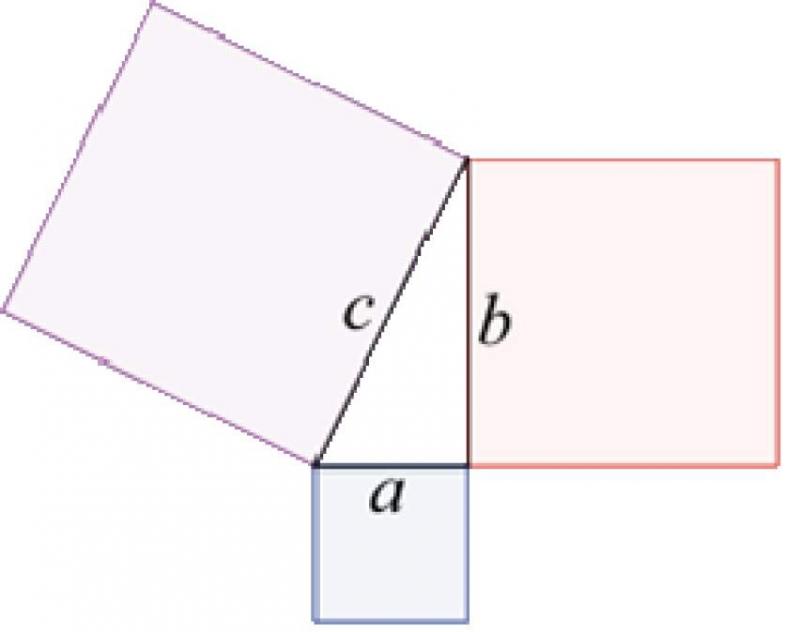
Düzbucaqlı üçbucaqda katetlərin kvadratları cəmi, hipotenuzun kvadratına bərabərdir. Katetləri a və b, hipotenuzu c ilə işarə etsək onda:

Aşağıdakı üçlüklər teoremin şərtlərini ödəyir.

Tərəfləri 3, 4 və 5 vahid olan üçbucağa bəzən Misir üçbucağı deyilir.
Katetlər üzərində qurulmuş kvadratların sahələri cəmi, hipotenuz üzərində qurulmuş kvadratın sahəsinə bərabərdir.
Tədqiqatın aparılması üçün qruplara verilən iş:
I qrup
1) Düzbucaqlı üçbucağın katetləri 8 və 15 sm olarsa, hipotenuzunu tapın.
2) Hipotenuzu 61 sm, katetlərindən biri 11 sm olan düzbucaqlı üçbucağın digər katetini tapın.
3) Diaqonalı 15 sm, tərəflərindən biri 9 sm olan düzbucaqlının perimetrini tapın.
II qrup
1) Hipotenuzu 37 sm, katetlərindən biri 35 sm olan düzbucaqlı üçbucağın digər katetini tapın.
2) Düzbucaqlı üçbucağın katetləri 7 sm və 24 sm olarsa, hipotenuzunu tapın.
3) Diaqonalı 17 sm, tərəflərindən biri 15 sm olan düzbucaqlının perimetrini tapın.
III qrup
1) Hipotenuzu 25 sm, katetlərindən biri 15 sm olan düzbucaqlı üçbucağın digər katetini tapın.
2) Düzbucaqlı üçbucağın katetləri 12 və 16 sm olarsa, hipotenuzunu tapın.
3) Diaqonalı 35 sm, tərəflərindən biri 28 sm olan düzbucaqlının perimetrini tapın.
İnformasiyanın mübadiləsi:
Qrup liderləri iş vərəqlərini təqdim edirlər.
Cavablar:
I qrup
1) 17 sm 2) 60 sm 3) 42 sm
II qrup
1) 12 sm 2) 25 sm 3) 46 sm
III qrup
1) 20 sm 2) 20 sm 3) 98 sm
İnformasiyanın müzakirəsi.
Müzakirə üçün suallar:
1. Pifaqor teoremi necə ifadə edilir?
2. Hansı üçbucaq Misir üçbucağı adlanır?
3. Bərabəryanlı düzbucaqlı üçbucağın hipotenuzu hansı düsturla hesablanır?
4. Tərəflər verildikdə üçbucağın düzbucaqlı olduğunu qabaqcadan demək olarmı?
Nəticə və ümumiləşdirmə:
Öyrəndik ki, katetlər verildikdə hipotenuz bu düstur vasitəsi ilə hesablanır:

Hipotenuz və katetlərdən biri verildikdə digər katet bu düstur vasitəsi ilə hesablanır:

Yaradıcı tətbiqetmə:
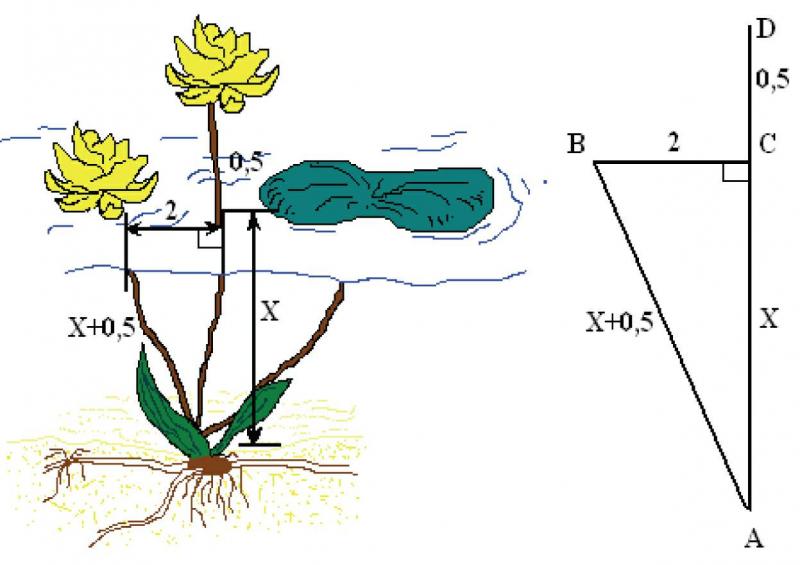
Göldə gövdəsi suyun səviyyəsindən yarım fut hündürlükdə nilufər gülü tənha boy atmışdı. Külək nəticəsində gül əyilir və gövdəsi suya batır. Balıqçı gülü əvvəlki yerindən 2 fut aralıda tapır. Gölün dərinliyini tapın.
1 fut = 0,3 m
Gölün dərinliyini X götürsək, AS=X olar.
Onda AD=AB=X+0,5 olar.
Pifaqor teoreminə görə, ACB üçbucağında
AB2-AC2=BC2
(X + 0,5)2 - X2 = 22,
X2 + X + 0,25 - X2 = 4,
X = 3,75.
Gölün dərinliyi 3,75 fut olur. 1 fut=0,3 m
3, 75 x 0,3 = 1,125 (m)
Cavab: 3,75 fut və yaxud 1,125 m.
Ev tapşırığı: Dərslikdən məsələləri (№ 230-235) həll etmək
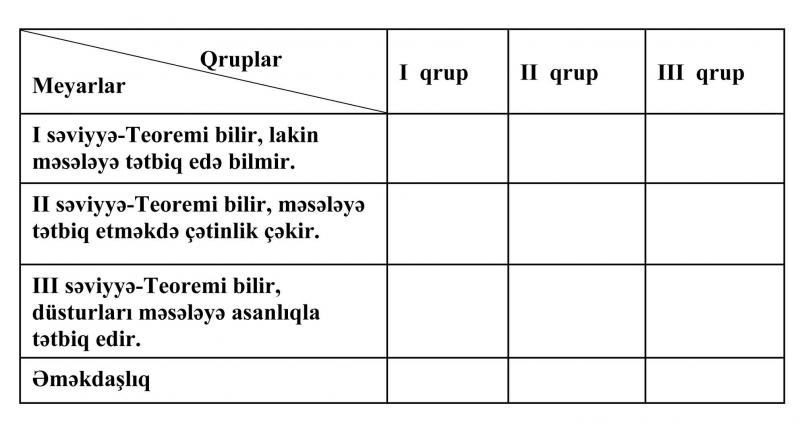
Qiymətləndirmə
Bibixanım CƏFƏROVA,
Bakı şəhər 265 nömrəli tam orta məktəbin müəllimi