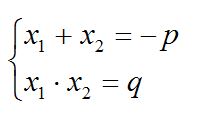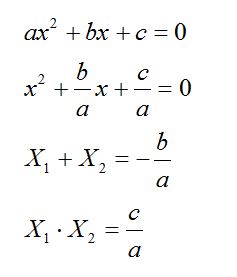Mövzu: Viyet teoremi

Standart:

2.1.1. Həyati situasiyaya uyğun kvadrat tənlik qurur.

2.2.2. Kvadrat tənlikləri həll edir.

Təlimin məqsədi: 

- kvadrat tənliyi Viyet teoremini tətbiq etməklə həll edir;

- verilmiş köklərinə görə kvadrat tənlik qurur;

- dəyişənlərinin qiyməti verilən kvadrat tənliyin kökləri olan ifadələri sadələşdirir və qiymətini hesablayır.

İş forması: Qruplarla iş

İş üsulu: Müsahibə və müzakirə

Resurslar: Dərslik, iş vərəqləri, İKT avadanlıqları

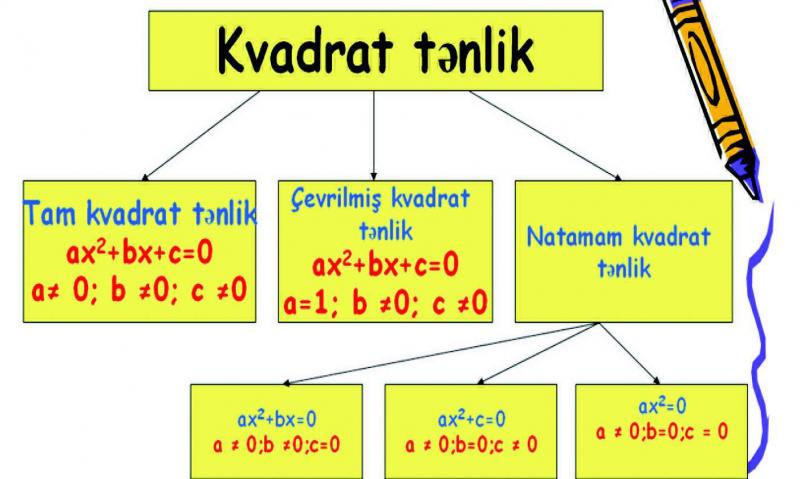
Mövzunun yaxşı mənimsənilməsi üçün şagirdlər “Kvadrat tənlik” mövzusunu yada salmalıdırlar.

Dərsin gedişi: Düşünməyə yönəltmə mərhələsində sinfi üç qrupa ayırmaqla fəal təlim üsullarından istifadə etmək.

Hər üç qrupun tapşırığı proyektor vasitəsilə lövhədə göstərilir və vərəqdə qrupun üzvlərinə paylanır.

I qrupun üzvlərindən biri kvadrat tənliklər haqqında danışır:

Kvadrat tənliyə aid məsələlərə 499-cu ildə hind riyaziyyatçısı və astronomu Ariabxatta tərəfindən tərtib olunmuş “Ariabxatta” astronomik traktında rast gəlinir. Digər hind alimi Braxmaqupta (VII əsr) ax²+bx+c, a>0 Kanonik şəkilli kvadrat tənliyin həllinin ümumi qaydasını şərh etmişdir. Braxmaquptanın verdiyi həll üsulu müasir üsulla demək olar ki, eynidir.

VIII-IX əsr özbək riyaziyyatçısı Məhəmməd Əl-Xarəzmi “Kitab əl-Cəbr vəl-Mükabala” əsərində xətti və kvadrat tənliklərin aşağıdakı 6 şəklini vermişdir:

Xarəzmi mənfi ədəddən istifadə etmədiyindən, bu tənliklərin hər bir həddi toplanan kimi qəbul olunurdu.

Kvadrat tənliyin Əl-Xarəzmi tərəfindən verilmiş qaydada həlli düsturu Avropada ilk dəfə 1202-ci ildə italyan riyaziyyatçısı Leonardo Fibonaççinin “Abak kitabı”nda şərh edilmişdir.

x²+bx=c şəklinə gətirilən kvadrat tənliyin həllinin ümumi üsulu alman riyaziyyatçısı M.Ştifel (1487-1567) tərəfindən şərh edilmişdir. Ümumi şəkildə kvadrat tənliyin həlli düsturunun çıxarılması ilə Viyet məşğul olmuşdur. Lakin o öz fikrini ancaq müsbət köklər üçün söyləmişdir. O, mənfi ədədləri qəbul etmirdi. Niderland riyaziyyatçısı A.Jirar (1595-1632), həmçinin Dekart və Nyutonun əsərlərindən sonra kvadrat tənliklərin həlli üsulu müasir şəkil almışdır.

Tənliyin köklərinin əmsallarından asılılığını ifadə edən düsturlar 1591-ci ildə Viyet tərəfindən çıxarılmışdır. Kvadrat tənlik üçün Viyet teoreminin müasir görünüşü belədir: (a+b)x-x²=ab tənliyinin kökləri a və b ədədləridir.

II qrupun tapşırığı: Diskriminanta görə kvadrat tənliyin həllinin araşdırılması.

III qrupun tapşırığı: Çevrilmiş kvadrat tənliyin kökləri düsturunu yazmaq və köklərin X₁+X₂ cəmini və X₁ • X₂ hasilini tapmaq.

Qruplar tapşırıqlarını yerinə yetirib təqdimatlar edirlər.

Sonra ümumiləşdirmə aparılır, Viyet teoreminin sözlə ifadə edilməsi və düsturla yazılışı soruşulur.

Teorem (Viyet teoremi): Çevrilmiş kvadrat tənliyin köklərinin cəmi əks işarə ilə götürülmüş ikinci əmsala, köklərinin hasili isə sərbəst həddə bərabərdir.

III qrupun üzvlərindən biri fransız riyaziyyatçısı Fransua Viyet haqqında danışır.

Fransua Viyet (1540-1603) - fransız riyaziyyatçısıdır, cəbri simvollar sistemini daxil etmiş, elementar cəbrin əsaslarını işləmişdir. O, ilk dəfə olaraq ədədləri hərflərlə işarə etmişdir (bu isə tənliklər nəzəriyyəsinin xeyli inkişaf etməsinə səbəb olmuşdur).

Viyet 1540-cı ildə Fransanın Vendes əyalətində Ventenay Ze Kombidə anadan olmuşdur.

O, hüquqşünas olandan sonra riyaziyyatla, astronomiya və kosmologiya ilə məşğul olmağı davam etdirmiş, 1571-ci ildə triqonometriyaya əlavə ilə birlikdə “riyazi kanon” çap etdirmişdir. 1591-ci ildə təkcə naməlum ədədlər üçün deyil, həm də əmsallar üçün bərabərliyin hərfi işarəsini daxil etmişdir. Bunun sayəsində ilk dəfə olaraq bərabərliklər və onların köklərini ümumi formula ilə işarə etmək mümkün olmuşdur. II, III və IV dərəcəli bərabərliklərin vahid üsulla həllinin təyini ona məxsusdur. Kəşflərinin içərisində Viyet bərabərliklərin köklər və əmsallar arasındakı asılılığının müəyyən edilməsi  yüksək qiymətləndirilmişdir.

Bərabərliklərin say əmsalları ilə yaxınlaşmış həlli üçün, Viyet Nyutonun sonradan təklif etdiyi metoda oxşayan metod təklif etmişdir. Triqonometriyada Viyet 3 verilənə görə hamar və sferik üçbucağın bütün elementlərinin tam həllini vermişdir. Cosinus nx və Sinus mx-in bütün dərəcələrində Cosinus x və sinus x-in mühüm açılışını tapmışdır. Viyet ilk dəfə olaraq sonsuz törəmələri nəzərdən keçirmişdir.

Viyet teoremi - göstərilən kvadrat tənliyin kökləri cəmi x-in əks işarəli əmsalına, kökləri hasili isə sərbəst həddə bərabərdir.

Düşünmə mərhələsində mövzunun nəzəri cəhətdən mənimsənilməsi yoxlanılır və çalışma həllinə tətbiqinə nail olunur.

Sonra şagirdlərlə sual-cavab aparılır:

Şagird: 

Sual: Kim Viyet teoreminin tərs teoremini ifadə edər?

Teorem:

Şagird: “İki m və n ədədlərinin cəmi (-p)-yə, hasili isə q-yə bərabərdirsə, m və n ədədləri x²+px+q=0 tənliyinin kökləridir” deyib isbat edir.

Sonra çevrilmiş kvadrat tənliyin köklərinin işarəsinin təyin edilməsi ilə bağlı iş aparılır.

Daha sonra Viyet teoreminin tətbiqinə aid lövhədə misallar həll olunur.

Tapşırıq icra edildikdən sonra ev işi elan olunur (dərslik, səh.100, tapşırıq № 10, 12, 14, 15)  və ona aid müəyyən izahlar verilir.

Refleksiya: Bu məqsədlə dərsdə keçirilənlər təkrarlanır, bacarıqlar yoxlanılır və dərs prosesində şagirdlərin fəaliyyəti dörd səviyyə üzrə qiymətləndirilir.

Viyet teoreminin tətbiq sahələri və çevrilmiş kvadrat tənliyin köklərinin işarəsinin təyin edilməsi proyektorla lövhədə göstərilir.

Tam kvadrat tənlik əvvəlcə çevrilmiş kvadrat tənliyə gətirilir, sonra Viyet teoremi tətbiq olunur.

Viyet teoremindən istifadə etməklə kvadrat tənlikləri həlletmə, verilmiş köklərinə görə kvadrat tənlik qurma, həmçinin bu köklər üzərində qurulmuş daha mürəkkəb ifadələri sadələşdirmə və qiymətini hesablama tapşırıqlarını yerinə yetirmə bacarıqlarına görə qiymətləndirmə aparılır.

Xalidə  SADIQOVA,

Bakı şəhərindəki fizika, riyaziyyat və informatika təmayüllü liseyin riyaziyyat müəllimi